Don’t mix up your "C-words"! Correlation & Causation explained

Introduction

Words get used informally in everyday life and (fingers crossed) more formally by professionals. Sometimes someone uses a word incorrectly, but you can understand what their intended meaning is from context. Often words that are used in a professional context have tightly defined and specific meanings in a particular field. 

This can lead to confusion and misinterpretation when people from different backgrounds are talking. Two words that are sometimes (wrongly) used interchangeably are: correlation and causation. But for scientists, engineers, mathematicians, and analysts their meanings are specific and somewhat different. 

I’m going to talk about how these words are similar but different when they are used technically. Because it’s what I know I naturally gravitate towards the context of marketing analysis, but the same will apply in lots of different contexts where relationships between factors are discussed, explored, and measured. 

What is correlation?

If two factors are correlated, then there is a link between them. Sometimes that is called an association or a relationship instead. In other words, if you were to plot a graph of the two things you would notice some similarity in their movements. When one goes up, the other goes up. Or when one goes up, the other goes down.

Temperature and ice cream sales are correlated. In the UK, the highest temperatures are in the summer months of July and August. Unsurprisingly, sales of ice cream are also highest in these months because more people like to eat ice cream when it is hot or when they are on holiday because the kids are not at school.  

Correlation coefficient

There is a way to measure the strength of the relationships between two things and it is often called the correlation coefficient. If you want to look up the formula it is also formally called “Pearson’s R” or “bivariate correlation.” If you aren’t interested in the mathematics, no problem, Excel has a formula you can use, called CORREL().

What the formula is doing, if you’re curious but want to avoid algebra, is looking at how closely the points fall on a straight line if you do a scatter plot of them. A scatter plot puts one thing on the horizontal axis (x) and the other on the vertical (y). Each point has two values: x and y. More related things show a more obvious and convincing pattern.

Here are some examples of perfect correlation that you rarely see in real life:

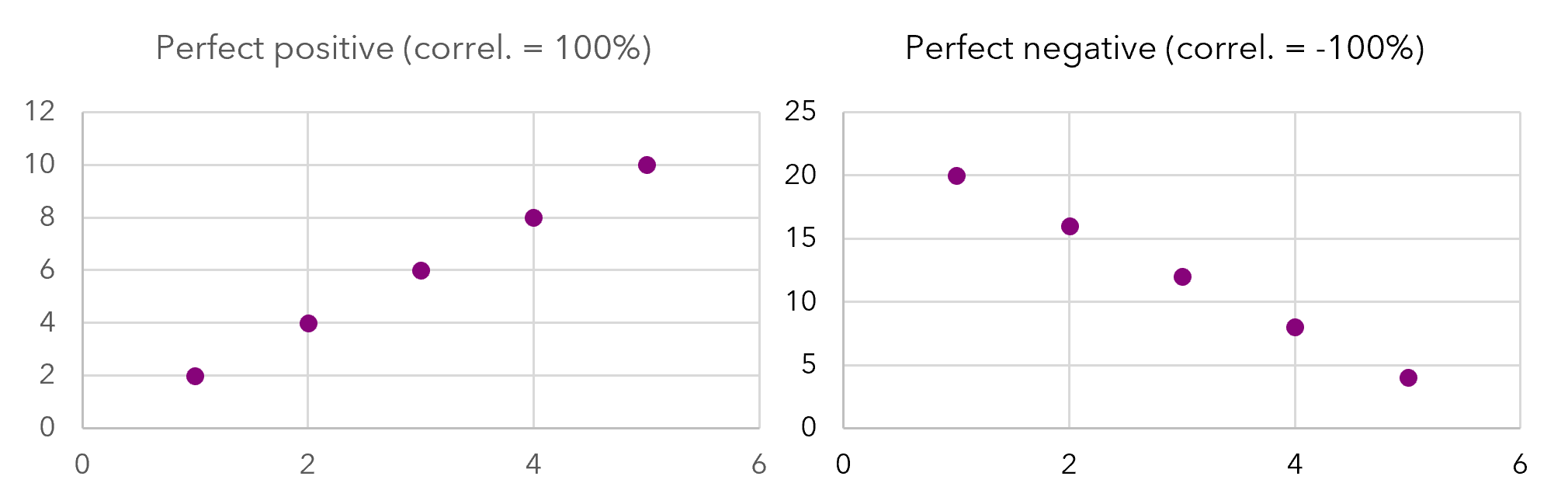
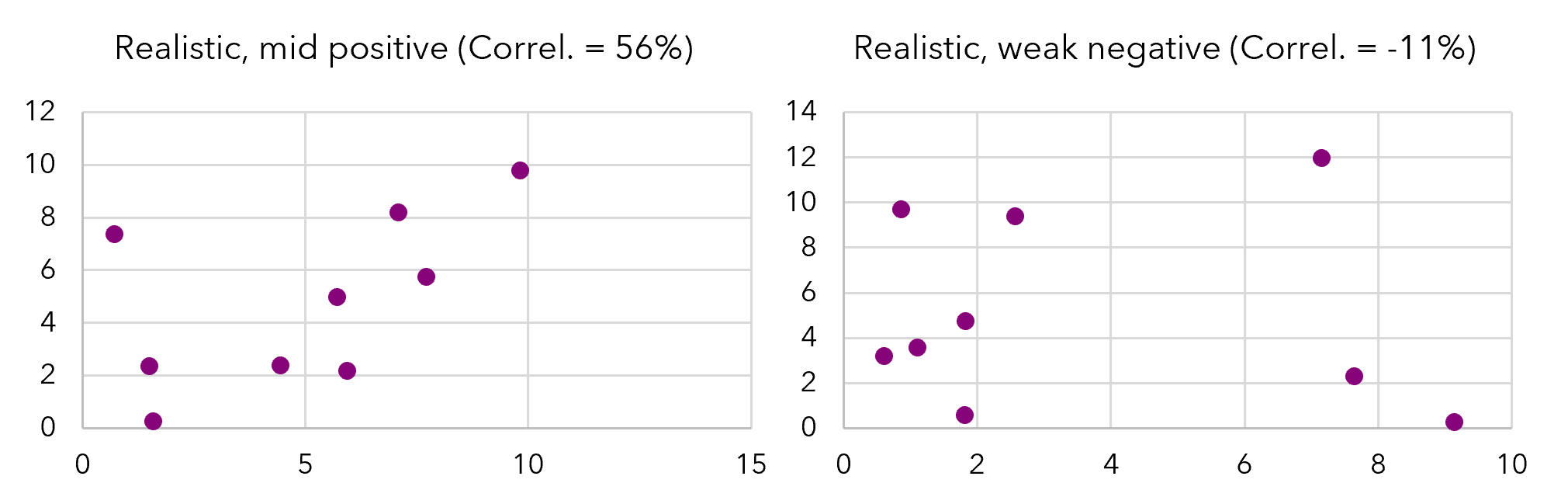
Two more realistic examples that you are more likely to find in real-world data:

Correlation myths

MYTH 1: a higher correlation (approaching 1 or -1) means that one causes the other. 

No. It just means there is a link and says nothing about cause. If there is a causal relationship, a correlation coefficient does not tell you in which direction that goes. Look at this chart of ice cream sales and shark attacks:

There is no causal link between these two things. It is simply because both ice cream and shark attacks are each causally related to temperature that they appear to be related.

MYTH 2: a stronger correlation between A and C than between B and C means that A has a bigger impact on C than B does. 

No. Correlations only tell you about the link between A and C when you ignore B - and all other factors that may affect C for that matter. You need to do a more complex multivariate analysis of some kind to work out relative impacts. Multivariate analysis allows for more than 2 factors to affect something at once. Which is much more like how the real world works.

MYTH 3: a negative correlation between two things means that if there is a causal relationship that will be negative too. 

No. The direction of a correlation is only an indication, not proof, of the direction of any causal relationship that exists between the two things. Before you start any analysis you should already have a view that is rooted in theory of whether to expect a positive or negative relationship. If you don't, how will you know that any data model you build is right?

MYTH 4: low or no correlation between two things means that there can be no causal relationship. 

No. Correlation only looks for simple relationships where a) x and y change at the same time and b) the pattern is linear, which means that every time x increases by 1, y increases or decreases by the same amount, for every successive increase in x. In the real world the link between two things is often more complicated, so a simple correlation appears weak.

For example, you perhaps know from the pandemic statistics that there is often a lag between things (infections and hospitalisations.) It takes a while for infected people to become sick enough to need hospital treatment, so as infections go up hospital admissions also go up, but in later weeks.

Some relationships are not straight-lined either which is all that a correlation coefficient measures. The spread of Covid-19 infections is an example of a curved relationship over time because each passing day the increase in number of infections keeps increasing. Because one infected person affects more than one other. The first graphic in this article makes this clear.

Correlation’s place in marketing analytics

With so many limitations, why is correlation analysis so popular? Anyone can do correlation analysis in Excel – it’s accessible and quick once you have data laid out in a suitable way. If you respect what it does and does not tell you it can be a cost effective first step to understanding more about what may impact what.

Looking for where your strongest correlations are gives clues about what the structure of your causal relationships are. If you get weak correlations it could be a sign that the relationships exist but are very complex. Correlation analysis helps to shape and focus more complex analysis that you may need to do to really determine the causal relationships. 

Be wary of those who dismiss correlation analysis outright and jump straight into more complicated models. It is true that more advanced techniques are often needed to get to cause and effect. But if you cannot see even any tiny hints of a relationship with a simple analysis, how confident are you really that the complicated model reflects reality?  

What is causation?

A causes B if there is a convincing relationship after you have quantified all the other potential factors that may impact B. How on earth do you do that? Scientists do it with lab experiments where they can control conditions to prove that that only thing that could have changed B is A.

Marketers run experiments too. They may divide their mailing list randomly into two groups, send a different version to each and track which had the higher response. The idea is that the copy was the only thing different in each group, so the copy difference is the cause. That approach is called A | B testing.

Or perhaps a brand measures the impact of radio, by not running radio in a couple of areas. Providing that all other things that affect sales is similar across those areas for the duration of the campaign, comparing sales across “radio” and “no radio” areas, gives a good read on the impact of radio. In both examples, marketers are trying to recreate the lab in the real world. 

What about if your business questions are bigger picture than that and you want to understand your business performance more broadly? For the average business you can probably make a long list of all the things that might make sales higher or lower from one week to the next. 

How do you disentangle all that?

There are lots of advanced data approaches to quantify causal relationships and use that knowledge to help you make smarter and more profitable decisions. Which approach you need to use really depends on what your questions are. I am a practitioner in just one of them and you can read more about that here.

When causality really matters

Because correlations are simple and indicative, basing your strategy on data evidence that is based only on correlations and not causal relationships is a gamble. If you do that anyway, make sure to review and recalculate those correlations regularly to check that they still hold. If they change, you should probably start digging to understand why. 

A common question I am asked is what size a business needs to be to benefit from advanced analysis. It’s less about the scale of your business and more about the scale of decisions that you want to or need to make and whether you are currently stuck on a decision. Often, the fee for analysis is relatively small in comparison to the potential revenue gain or cost saving. 

Causal analysis enables you to understand how you can pull levers in your business to drive change and or mitigate against factors out of your control. It is often deemed an unnecessary expense when business is good. Really, that is the best time to invest in analysis so that what the models capture is the recipe for success rather than a snapshot of your worst times. 

Wrapping it up

If A causes B, then there will usually be a correlation between A and B. But it is not necessarily true that if there is a correlation between A and B that A causes B. B may cause A. Or neither causes the other, they just happen to move similarly. It is exactly because these terms are “sort of similar” that confusion arises!

It is important to understand the difference if you are using data to make big decisions. I have seen many examples in my career of businesses taking huge financial decisions on shaky analytical foundations because they have assumed that the correlation coefficient between two factors meant that one caused the other.

There are also perhaps not enough people who understand the benefits of simple correlation analysis. It can guide you a lot. Providing you respect the limitations it can play a useful role in your data and insight strategy. The fact that some form of correlation analysis plays a part in most advanced analytics projects is no accident.

Please ask before reproducing my material partially or wholly for commercial use.
© Jo Gordon Consulting Ltd 2021